CHAPTER 1
EXPRESSIONS AND FORMULAS
ONE VARIABLE EQUATIONS AND INEQUALITIES
|
| 1.- Expressions and Formulas: Order of Operations.* |
| 2.- Real Numbers: Properties of Numbers, and Number Sets.* |
| 3.- One Variable Linear Equations Including Absolute Value.* |
| 4.- One Variable Linear Inequalities Including Absolute Value.* (For Inequalities Real World Applications lesson.* See chapter 7) |
| 5.-Inequalities Real World Applications.* |
CHAPTER 2
RELATIONS AND FUNCTIONS
SYSTEMS OF TWO VARIABLE EQUATIONS AND INEQUALITIES
|
| 1.- Relations and Functions.* |
| 2.- Introduction to Slope of a Line.* |
| 3.- Two Variable Systems of Linear Equations.* |
| 4.- Two Variable Systems of Linear Inequalities.* |
CHAPTER 3
OTHER WAYS TO SOLVE SYSTEMS OF LINEAR EQUATIONS
LINEAR PROGRAMING
|
| 1.- Using Determinants to Solve Systems of Linear Equations: Cramer's Rule. |
| 2.- Using Augmented Matrix to Solve Systems of Linear Equations. Introduction of Matrices and their operations. |
| 3.- Linear Programing: Using a Set of Conditions to Create a Polygon and Using the Vertices to Optimize an Optimizing Function. |
CHAPTER 4
ARITHMETIC OF POLYNOMIALS AND PROPERTIES OF EXPONENTS
RADICAL EQUATIONS AND ONE INTRODUCTION TO COMPLEX NUMBERS.
This section is under editing. Since around 2014 this site experience a string of hacks and many files were affected.
The first three lessons that deal with arithmetic with polynomials were particularly affected and the original PowerPoint files lost.
For the lessons to be edited they need to be in the original PowerPoint format since the format posted is HTML5 and does not allow editing them.
Originally the first lessons were in a page for Algebra 1 and another for Algebra 2. We combined the lessons in Algebra 1/2 and these first lessons
somehow have repetitive content in the areas where alg1 and alg2 overlapped. We will have practically to rewrite them in full to eliminate that situation.
Lessons about arithmetic of polynomials are particularly time consuming. Hopefully in a few weeks the problem will be fixed.
|
| 1.- Adding, Subtracting, Multiplying and Dividing Polynomials 1* |
| 2.- Adding, Subtracting, Multiplying and Dividing Polynomials 2* |
| 2.- Adding Polynomials: Same as lesson above but more control since advances by clicks not automatically. Hackers deleted the one before. We will have to redo it to give back manual control. |
| 3.- Algebra Tiles Adding Polynomials* (modeling: Concrete to abstract) |
| 4.- Algebra Tiles Multiplying and factoring Polynomials* (modeling: Concrete to abstract) |
| 5.- Properties of Exponents. Adding, Subtracting, Multiplying and Dividing.* |
| 6.- Simplifying Numeric Rational and Irrational Radicals.. Learn to simplify numerical radical expressions, multiply and divide them. |
| 7.- Rational Exponents and Radicals. Adding, Subtracting, Multiplying and Dividing. Including expressions with variables. |
| 8.- Radical Equations and Inequalities. Determining valid domain and solution.* |
| 9.- Complex Numbers. Adding, Subtracting, Multiplying and Dividing. |
CHAPTER 5
ANALYTIC GEOMETRY
CONICS: PARABOLA, CIRCLE, ELLIPSE, HYPERBOLE
|
| 1.- Quadratic Functions.* |
| 2.- Discriminant and Sum & Product of Roots.* |
| 3.- Distance Formula, and Midpoint Formula.* |
| 4.- Parabola: From Graph to Equation and From Equation to Graph. |
| 5.- Circle: From Graph to Equation and From Equation to Graph. |
| 6.- Ellipse: From Graph to Equation and From Equation to Graph. |
| 7.- Hyperbole: From Graph to Equation and From Equation to Graph. |
| 10.- Inequalities with All Conics. |
CHAPTER 6
REAL WORLD APPLICATIONS AND PROOFS
FOR CONICS AND POLYNOMIAL FUNCTIONS AND INEQUALITIES
|
| 1.- Conic Sections ad Their Generator |
| 2.- Conic Sections and The General Equation for Conics. |
| 3.- Parabola Formula Proof. |
| 4.- Ellipse Formula Proof. |
| 5.- Hyperbole Formula Proof. |
| 6.- A Ball Up to a Ramp Generates a Parabolic Model.* |
| 7.- Animation for the Ball Up to a Ramp (Vernier LabPro 2) |
| 8.- Finding the Maximum Area of a Rectangle with 24 wood sticks. Quadratic Model: Parabola* |
| 9.- Geometry and Algebra to Represent Arithmetic with Polynomials using Base 10 or Foam Prisms.* |
CHAPTER 7
FUNCTIONS THAT INVOLVE POLYNOMIALS
|
| 1.- Polynomials and Zeros, Roots or Solutions (Intersections with x-axis) |
| 2.- Mathematical Models Activity that Yields Polynomial Functions. |
3a.- It is very similar to activity in previously named as 7_1a_mathematical-models but with a connection to topics dealt in precalculus and calculus that may be teach to students to gives them the look into the future as demanded by the COMMON CORE STANDARDS and previously by the old CALIFORNIA STANDARDS of the 2000's.
3b.- Lesson that introduces the algebraic and coordinate geometric link to calculus demanded by the COMMON CORE STANDARDS and previously by the old CALIFORNIA STANDARDS of the 2000's for the first and second derivatives (Recommended to study or view before the lesson in 3a
|
| 4.- Rational Zero Theorem |
| 5.- Quadratic Techniques to Solve Polynomial Functions of Higher Degree. |
| 6.- Composition of Functions, and Inverse of Functions. |
| 7.- Pascal's Triangle for Binomial expansion visual and with combinations formula. |
|
INSIDE EACH LESSON YOU MAY DO AS THIS GRAPHIC SHOWS
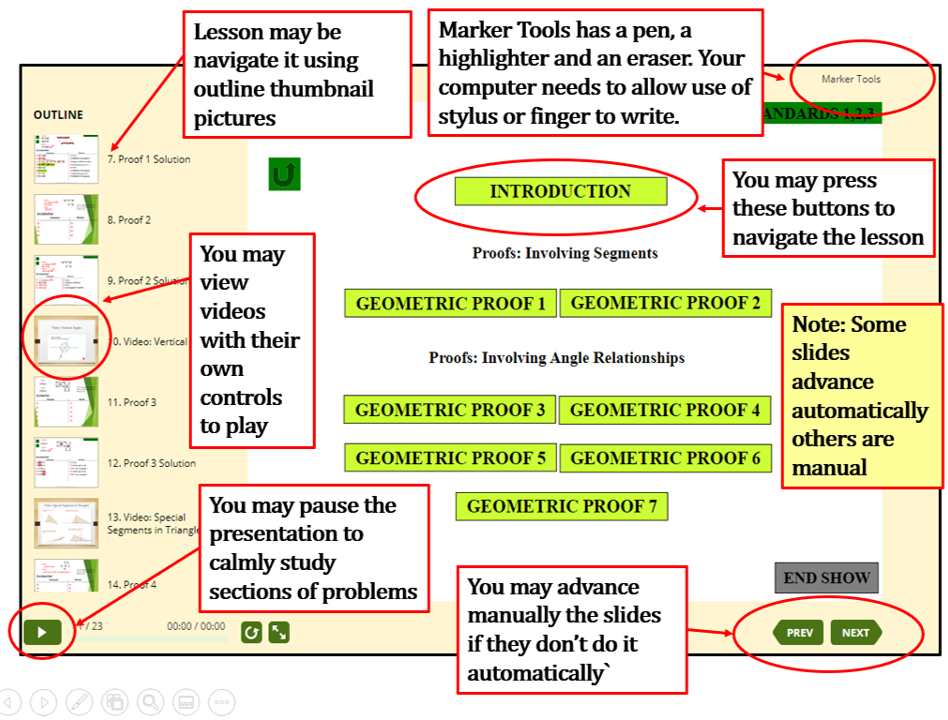
|
CHAPTER 8
RATIONAL EQUATIONS, EXPONENTIAL AND LOGARITMIC EQUATIONS
AND AN INTRODUCTION TO SEQUENCES AND SERIES (ARITHMETIC AND GEOMETRIC)
|
| 1.- Rational Equations.* |
| 2.- Base Number Systems Introduction: Base 10 to Base 2, Binary and Base 20. Converting between basis and Basic Math Operations with Properties of Real Numbers and Properties of Equality. |
| 3.- Base Number Systems Introduction: Arithmetic Operations |
| 4.- Arithmetic Operations With Base 16 or Hexadecimal in particular Multiplications |
| 5.- Arithmetic Operations With Base Different than base 10: Divisions |
| 6.- Exponential and Logarithmic Equations. |
| 7.- Lesson focused on Arithmetic Sequences and Series including the corresponding proofs both the algorithmic solution and the geometric implications in coordinate geometry. |
| 8.- Lesson focused on Geometric Sequences and Series including the corresponding proofs both the algorithmic solution and the geometric implications in coordinate geometry |
| 9.- Lesson focused on Quadratic Sequences including both the algorithmic solution and the geometric implications in coordinate geometry |
| 10.- Lesson presents some examples of applications for Arithmetic, Geometric and Quadratic Sequences |
| 11.- Lesson about reviewing how parameters in an exponential equation change and revisiting its relationship with geometric sequences as a subset of exponential equations but with a discrete domain whereas than the exponential equations have a continuous domain. |
CHAPTER 9
PROBABILITY AND STATISTICS TOPICS
(Topics in these lessons are also in the section for statistics)
|
| 1.- Measures of Central Tendency and Dispersion: Mean, Median and Mode. Standard Deviation and Variance. |
| 2.- Counting Principle. |
| 3- Combinations and Permutations. |
| 4.- Experimental Probability (Introduction) |
| 5.- Adding Probabilities (Module "OR") and Multiplying Probabilities (Module "AND") (From Informal to Formal) |
| 6- Binomial Probability. Calculated with the formula, the tables and with Ti-83 Texas Instrument Calculator. |
| 7- Normal Distribution: Introduction to Standard Normal Distribution and Z-score |
CHAPTER 10
PLAYING DICE, CARDS AND THE WHEEL OF FORTUNE.
A HANDS ON APPROACH TO LEARN PROBABILITY.
|
| 1.- Real World Probability with a Spinning Wheel. (You fill in the tables) |
| 2.- Real World Probability with a Spinning Wheel (Tables already fill) |
| 3.- Real World Probability with Dice and Cards (You fill the tables) |
| 3.- Real World Probability with Dice and Cards (Tables already fill) |
CHAPTER 11
ADVANCED TOPICS OF TRIGONOMETRY
|
| 1.- Trigonometry An In Depth Approach to Sine, Cosine, Tangent, Cotangent, Secant and Cosecant: Trigonometry Ratios and Their Graphs and Real World Applications. |
| 2.- Trigonometric Graphing of Functions with an emphasis in parameters. |
| 3.- Trigonometry Identities. Sum and Difference, Double Angle and Half Angle. PROOFS |
| 4.- Graphing Polar Functions: Limazon, Cardioid, Even or odd number of Leaves Rose (odd and even), Leminiscate, etc |
| 5.- Complex Roots and their graphs: with emphasis on phases and solution polygons. (Same lesson posted in trigonometry as Modeling in Trigonometry title.) |