CHAPTER 1
BASIC DEFINITIONS, ANGLE RELATIONSHIPS AND ANGLE PAIRS.
|
| 1.- Basic Geometric Definitions: Lines, Angles, Planes, Segment Addition Postulate, Midpoint, Distance Formula. |
| 2.- Complementary, Supplementary, Linear Pair, and Vertical Angles: Definitions and Algebraic Proofs with Geometry. |
| 3.- Angle Pairs: Complementary, and Supplementary Angles as Word Problems. |
| 4.- Angle Pairs with Geolegs (manipulatives hands on approach): Complementary, Supplementary and Vertical Angles. |
| 5.- Angle Pairs in Parallel Lines: Corresponding, Alternate Interior and Alternate Exterior, and Consecutive Interior Angles. |
CHAPTER 2
ANGLE RELATIONSHIPS IN PROOFS, INDUCTIVE AND DEDUCTIVE REASONING. SLOPE.
|
| 1.- Inductive and Deductive Reasoning: If - Then Statements, Law of Syllogism and Law of Detachment. |
| 2.- Two Column Proofs Involving Segment and Angle Relationships: Two Column Proofs and Flow Proofs with Segment Addition Postulate and Angle Pairs. |
| 3.- Converting Two Column Proofs to Paragraph Proofs: An introduction to Paragraph Proofs using two column proofs. |
| 4.- Slope Introduction: Slope of a Linear Equation. Horizontal, Vertical, Falling to the Right or to the Left. Parallel vs Skew Lines. Parallel and Perpendicular Planes. |
CHAPTER 3: TRIANGLES
PROVING TRIANGLES CONGRUENT AND TRIANGLE INEQUALITY.
|
| 1.- Proving Triangles Congruent: Algebraic - Geometric Proofs to Prove Triangles Congruent. |
| 2.- Proving Triangles Congruent: SSS, ASA, SAS, AND AAS. |
| 3.- Two Column Proofs Involving Triangle Congruence: Two Column Proofs and Flow Proofs using Angle Relationships and SSS, ASA, SAS, and AAS. |
| 4.- One and Two Triangle Inequality Theorems: Ordering sides and Angles Using Triangle Inequality. |
| 5.- Drilling in Geometric Statements: Congruent Geometric Statements and How to Write them and Read them Properly. |
| 6.- Introduction to proofs by contradiction in paragraph format and two-column format |
CHAPTER 4
QUADRILATERALS AND THEIR PROPERTIES IN GEOMETRIC AND ALGEBRAIC PROOFS.
|
| 1.- Properties of Quadrilaterals: Squares, Rhombi, Rectangles, Parallelograms and Trapezoids. |
| 2.- Proving Properties of Special Quadrilaterals using Congruent, or Isometric, or Rigid Transformations. |
| 3.- Segments and Angles in Parallelograms: Problems Involving Angles and Segments in Regular Parallelograms and Rectangles. |
| 4.- Segments and Angles in Squares and Rhombi: Problems that Include Angles and Segments in Squares and Rhombi. |
| 5.- Segments and Angles in Regular and Isosceles Trapezoids: Problems Deal with Segments and Angles in Trapezoids. |
| 6.- Two Column Proofs with Quadrilaterals and Triangles: Solving Two Column Proofs and Flow Proofs Using Properties of Parallelograms and Quadrilaterals and Properties of Triangles to Prove Congruence Statements and Segment or Angle Relationships. |
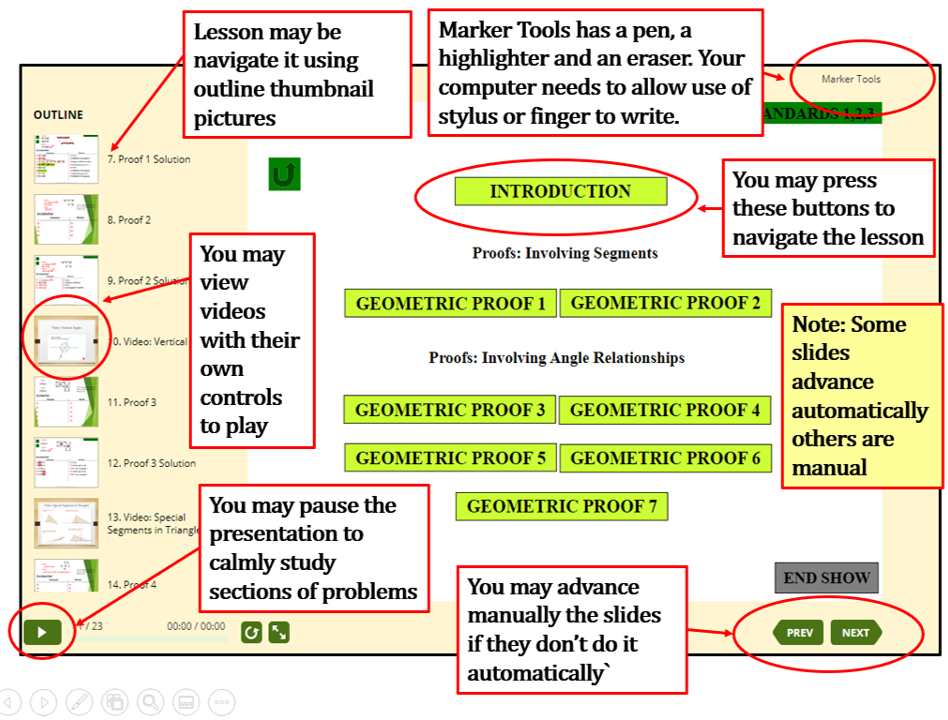
INSIDE EACH LESSON YOU MAY DO AS THIS GRAPHIC SHOWS
CHAPTER 5
PROPORTIONAL REASONING SIMILARITY AND TRIGONOMETRY.
|
| 1.- Similarity Theorems AA, SAS and AAA. Similarity Applied to Two Triangles and Lines Cut by Transversals. |
| 2.- Similarity Theorems Involving Special Segments In Triangles: Atltitudes, Medians, Angle Bisectors and Perpendicular Bisectors Similarity Relationships in Triangles. |
| 3.- Similarity Applied in a Right Triangle: Drawing a height to the Right Angle of A Right Triangle. |
| 4.- Proofs in Two Column Format involving similarity in triangles. Two Column Proofs and Flow Proofs for Similarity. |
| 5.- 30°-60°-90° and 45°-45°-90° Triangles: This lesson deals with special right triangles from the geometric informal proof to solution of some examples and very soon we are going to add suggested application problems. It has a set of videos to review concepts used in the proofs like special lines and segments in triangles, Pythagorean Theorem, and since browsers dropped the support for applets a few videos of applets than by themselves constitute a very robust dynamic geometric proof. |
| 6.- Similarity in Special Right Triangles using Dilations Enrichment Lesson. See dilation lessons at bottom of this webpage before visiting this. |
| 7.- Right Triangle Trigonometry: Right Triangle Ratios of Sine, Cosine and Tangent Applied to Solutions of Problems Involving Segments and Angles. |
| 8.- Laws of Sines and Cosines: Trigonometry Applied to Acute and Obtuse Triangles Using the Laws of Sine and Cosine. |
| 9.- Learning about angle measurement units: Radians and degrees in coterminal sides using special right triangles 30°- 60°-90° and 45°-45°-90° |
CHAPTER 6
ANGLES, ARCS AND SEGMENTS IN CIRCLES.
|
| 1.- Basic Definitions For Circles: Arcs, Chords, Central Angles, Inscribed Angles and Arc Addition Postulate. |
| 2.- Theorems Involving Congruent Chords and Intersecting Chords in Circles. Applied to Individual Circles or Several Circles. |
| 3.- Inscribed and Central Angles: Problems that Focus in Inscribed and Central Angles Usings Triangles and Parallelograms. |
| 4.- Arcs and Angles Formed by Secants, and Tangents in a Circle: Segments that Give Place Secant and Tangents in Circles and the Angles and Arcs that They Form in the Circle Intersecting Inside, On or Outside the Circle. |
| 5.- Segment Relationships Created by Chords, Secants and Tangents. Chords, Secants and Tangents and the Segments that They Create When Intersecting Inside, On or Outside the Circle. |
| 6.- Geometric Two Column Proofs Involving Circles with Chords, Tangents and Secants Part 1. |
| 7.- Geometric Two Column Proofs Involving Circles with Chords, Tangents and Secants Part 2. |
CHAPTER 7
AREAS IN POLYGONS (REGULAR AND IRREGULAR)
|
| 1.- Angle Measure in Polygons: Interior and Angles in Polygons. |
| 2.- Calculating Areas in Parallelograms and Rectangles. |
| 3.- Calculating Areas in Rhombi, Trapezoids and Triangles. |
| 4.- Areas of Triangles: Special Cases. Involving Pythagorean Theorem, Special Right Triangles and Trigonometry. |
| 5.- Calculating Areas of Regular Polygons: Areas of Equilateral Triangles, Squares, Pentagons, Hexagons, etc. |
CHAPTER 8
SURFACE AREA AND VOLUME (PLATONIC SOLIDS)
|
| 1.- Finding Surface Area and Volume of CYLINDERS. |
| 2.- Finding Surface Area and Volume of PRISMS. |
| 3.- Finding Surface Area and Volume of Solids Built with Base 10 Blocks. |
| 4.- Finding Surface Area and Volume of CONES. |
| 5.- Finding Surface Area and Volume of PYRAMIDS. |
| 6.- Finding Surface Area and Volume of SPHERES. |
CHAPTER 9
SURFACE AREA AND VOLUME COMPOSITE SOLIDS
PLATONIC SOLIDS TOGHETER AND/OR REMOVED ONE FROM THE OTHER
|
| 1.- Calculating Surface Area and Volume of Composite Solids by Adding Solids. |
| 2.- Calculating Surface Area and Volume of Composite Solids by Subtracting Solids. |
| 3.- Calculating Surface Area and Volume of Composite Solids by Adding and Subtracting Solids. |
| 4.- Calculating Surface Area and Volume of Composite Solids in buildings to estimate areas to give maintenance and volumes to dimension AC units for example. Applications in the machining shop. |
CHAPTER 10
PLANE GEOMETRY AND CALCULUS IN SURFACE AREA AND VOLUME
OF SOLIDS OF REVOLUTION AND MATHEMATICAL MODELS INVOLVING SOLIDS.
|
| 1.- Surface Area of Solids of Revolution Using Plane Geometry and Calculus. |
| 2.- Volume of Solids of Revolution Using Plane Geometry and Calculus. |
| 3.- Animation of Area Revolving and Forming a Solid Of Revolution. |
| 4.- Mathematical Modeling with Two Halves of a Bottle Calculating Surface Area and Volume From the Math Model. |
CHAPTER 11
BASIC CONSTRUCTIONS AND TRANSFORMATIONS
WITH PLANE GEOMETRY AND THE COORDINATE PLANE.
|
| 1.-Introduction to Basic Constructions Using Compass and Ruler or Straight Edge/Protractor. This lesson takes you step by step (click by click) through the constructions. |
| 2.-Basic Construction Videos: Perpendicular Bisector and Perpendiculars to a point, Angle Bisector. These lessons are videos that may be paused or back/for-warded. |
| 3.-Basic Construction Videos: 30°, 45°, and 60° Angles, and Equilateral Equiangular Triangle. These lessons are videos that may be paused or back/for-warded. |
| 4.-Basic Construction Videos: Parallel Lines, Regular Polygons (Equilateral Triangle and Hexagon) These lessons are videos that may be paused or back/for-warded. |
| 5.- Constructing a Triangle Circumscribing a Circle (Incenter) |
| 6.- Constructing a Circle Circumscribing a Triangle (Circumcenter) |
| 7.- Translations with Plane Geometry. |
| 8.- Rotations with Plane Geometry. |
| 9.- Reflections with Plane Geometry. |
| 10.- Translations in the Coordinate Plane. |
| 11.- Rotations in the Coordinate Plane. |
| 12.- Reflections in the Coordinate Plane. |
| 13.- Hands-On Transformations Using Geoboards and the Coordinate Plane. |
| 14.- Using Technology and Mainboards with 1/8 square Grid to Perform Animation of a Doll. |
| 15.- Transformations application. Planes flying over yosemite national park |
| 16.- Reflecting half a polygon along its line of symmetry when reflected points can not be obtained by counting in the grid. |
| 17.- Lesson about Non-Congruent Transformations or Dilations. |
| 18.- Lesson about composition of congruent transformations. |
| 19.- Lesson about Rotational Symmetry: Order of Rotational Symmetry, Line Symmetry, Point Symmetry on regular and irregular convex. |
| 20.- Lesson about an application to get a printout of a blueprint with the proper scale using PowerPoint or Google Earth and calculating the areas using Google Earth of a parcel and its structures |
| 21.- Construct Regular Polygons by Approximation in a touch-screen with no compass needed. |
| 22.- Videos about Merging the digital tools of a mini-iPad with physical compass, ruler or straightedge and protractor in geometric constructions. |
| 23.- Performing proofs with compass and ruler and presenting afterwards of other proof formats. |
